培地成分を対象としたベイズ最適化の活用入門（バッチ最適化編）

■はじめに

前回の記事では、逐次最適化を用いて、ラウンドごとに1条件ずつ生成し、その都度モデルを更新していくアプローチを紹介しました。しかし実際の実験では、1ラウンドで複数の条件を並行して試すことが一般的です。そこで今回は、そのような「バッチ最適化」の実装例を紹介していきます。

＊前回の逐次最適化についてはこちらから

今回も細胞シミュレーションのために、前回登場した「細胞くん」を対象に、最適な培地条件を探索します。振り返りとして、この「細胞くん」関数はグルコース量を x、窒素源 NH₄Cl を y として、ある挙動を示す2次元関数です。分布は以下のようになります。

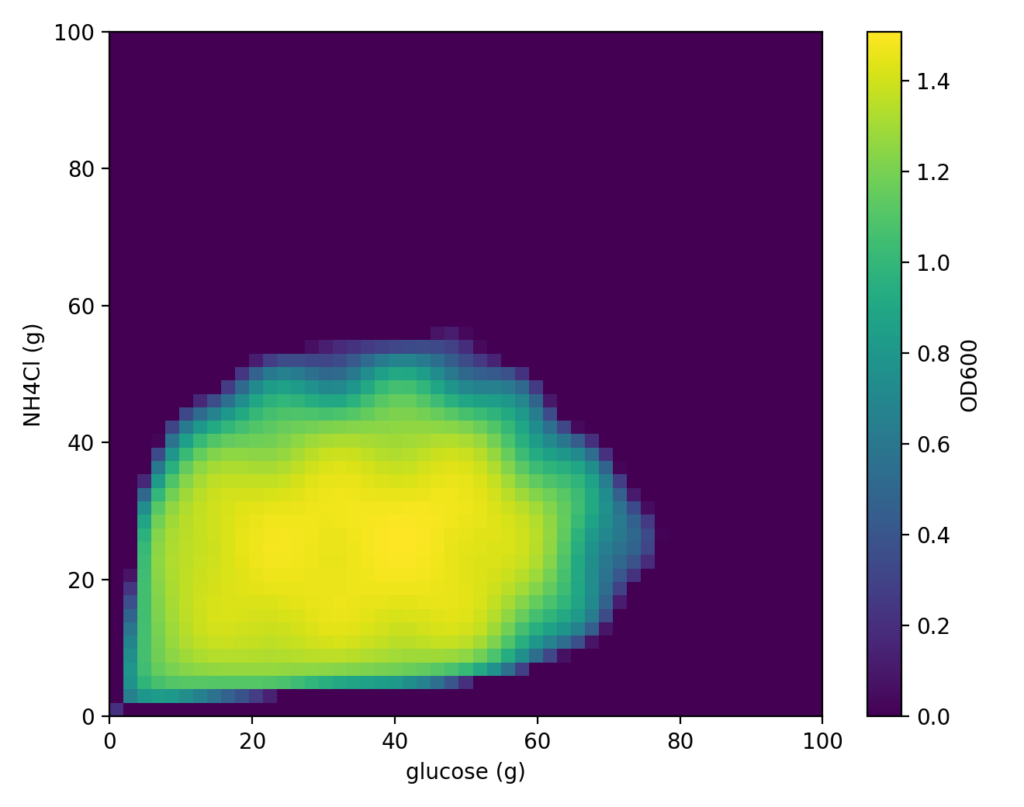
細胞くんのグルコースとNH₄Cl量に対する応答をシミュレーションした関数の分布

前回に引き続き、初期データとして、以下の実測値を設定します。

以降のスクリプトは、次のリンクから実行できます

https://colab.research.google.com/drive/1BJMlmY7arYF2zNQgnbbC_93nksJW9_4F?usp=sharing

まず解析に必要なパッケージ群をインストールします。

!pip -q install imageio openpyxl scikit-optimize

次に、初期データをPythonで利用可能なデータフレームに読み込みます。

import pandas as pd
from io import StringIO

csv_text = """Glucose (g),NH4Cl (g),0D600
2.5,2.5,0.761678
2.5,5,0.874593
2.5,7.5,0.879424
5,2.5,0.902424
5,5,1.079207
5,7.5,1.128299
"""

# 文字列CSV → DataFrame
df_raw = pd.read_csv(StringIO(csv_text))

# 列名を標準化：x=glucose, y=NH4Cl, od=OD600
seed_df = df_raw.rename(columns={"Glucose (g)": "x", "NH4Cl (g)": "y", "0D600": "od"})

# 確認
seed_df

続いて、ベイス最適化に用いるモデルを準備します。

from od_objective_2d import ODObjective2D, BOUNDS2D
from skopt import Optimizer
from skopt.space import Real
import numpy as np

obj = ODObjective2D()
space = [Real(BOUNDS2D["x"][0], BOUNDS2D["x"][1], name="x"), #BOUNDS2D：探索範囲（x=glucose, y=NH4Cl の下限/上限）。
         Real(BOUNDS2D["y"][0], BOUNDS2D["y"][1], name="y")] #space：skopt に渡す連続2次元の探索空間（Real で実数範囲を指定）。

opt = Optimizer(dimensions=space, base_estimator="GP", acq_func="EI", random_state=42)

ここで

ODObjective2D は「細胞くん」の挙動を模擬する関数です。実際の実験ではこの部分をスキップし、実測値を代わりに入力します。

■バッチ最適化の実行

ここから前回の実装と変わっていきます。

n_rounds = 10      # ラウンド数（各ラウンドで batch_size 個の条件を提案）
batch_size = 2     # 1ラウンドで何条件提案するか

print("\n=== ベイズ最適化（バッチ提案）を開始 ===")
for r in range(1, n_rounds + 1):
    # 1) ask: 次に測るべき点を batch_size 個まとめて提案
    X_next = opt.ask(n_points=batch_size, strategy="cl_min")
    print(f"[BO round {r}] 提案点:")
    for j, (x_next, y_next) in enumerate(X_next, start=1):
        print(f"  cond{j}: Glucose={x_next:.3f}, NH4Cl={y_next:.3f}")

    # 2) 実験（デモ: 目的関数で代用。実運用では実測ODに置換）
    od_list = [float(obj(xn, yn)) for (xn, yn) in X_next]
    for j, odm in enumerate(od_list, start=1):
        print(f"    → cond{j} 測定 OD= {odm:.6f}")

    # 3) tell: まとめて BOモデル に渡す
    opt.tell(X_next, [-od for od in od_list])

    # 4) ベスト更新チェック & ログ追加
    for j, ((xn, yn), odm) in enumerate(zip(X_next, od_list), start=1):
        improved = ""
        if odm > best_od:
            best_od, best_xy = odm, (xn, yn)
            improved = "  ← ★ベスト更新！"

        rows.append({
            "iter": len(rows) + 1,
            "phase": "bo",
            "round": r,
            "cond_in_round": j,
            "x": xn,
            "y": yn,
            "od": odm,
            "best_so_far": best_od,
            "best_x": best_xy[0],
            "best_y": best_xy[1],
        })
        print(f"    cond{j}: 現在のbest = {best_od:.6f} @ {best_xy}{improved}")

# skopt 内部での最良点（-OD を最小化した結果）を確認
best_idx = int(np.argmin(opt.yi))
skopt_best_xy = tuple(opt.Xi[best_idx])
skopt_best_od = -opt.yi[best_idx]

print("\n=== 最終サマリ ===")
print(f"ログ上の best: OD={best_od:.6f} @ {best_xy}")
print(f"skopt の best: OD={skopt_best_od:.6f} @ {skopt_best_xy}")

今回は以下の設定で最適化を実施しました。

n_rounds = 10      # ラウンド数（各ラウンドで batch_size 個の条件を提案）
batch_size = 2     # 1ラウンドで何条件提案するか

各ラウンドで2条件ずつ提案し、それぞれを評価してモデルに反映させます。結果として得られた最適条件は以下の通りです。

=== ベイズ最適化（バッチ提案）を開始 ===
[BO round 1] 提案点:
  cond1: Glucose=41.010, NH4Cl=72.773
  cond2: Glucose=93.287, NH4Cl=31.580
    → cond1 測定 OD= 0.000000
    → cond2 測定 OD= 0.000000
    cond1: 現在のbest = 1.128299 @ (5.0, 7.5)
    cond2: 現在のbest = 1.128299 @ (5.0, 7.5)
[BO round 2] 提案点:
  cond1: Glucose=83.739, NH4Cl=88.332
  cond2: Glucose=30.341, NH4Cl=95.122
    → cond1 測定 OD= 0.000000
    → cond2 測定 OD= 0.000000
    cond1: 現在のbest = 1.128299 @ (5.0, 7.5)
    cond2: 現在のbest = 1.128299 @ (5.0, 7.5)
    
 ~中略~
 
 [BO round 10] 提案点:
  cond1: Glucose=47.392, NH4Cl=36.881
  cond2: Glucose=44.905, NH4Cl=32.587
    → cond1 測定 OD= 1.419688
    → cond2 測定 OD= 1.462368
    cond1: 現在のbest = 1.495663 @ (43.39859641296826, 27.89400149397207)
    cond2: 現在のbest = 1.495663 @ (43.39859641296826, 27.89400149397207)

バッチ最適化の様子を以下の折れ線グラフにまとめてみました。

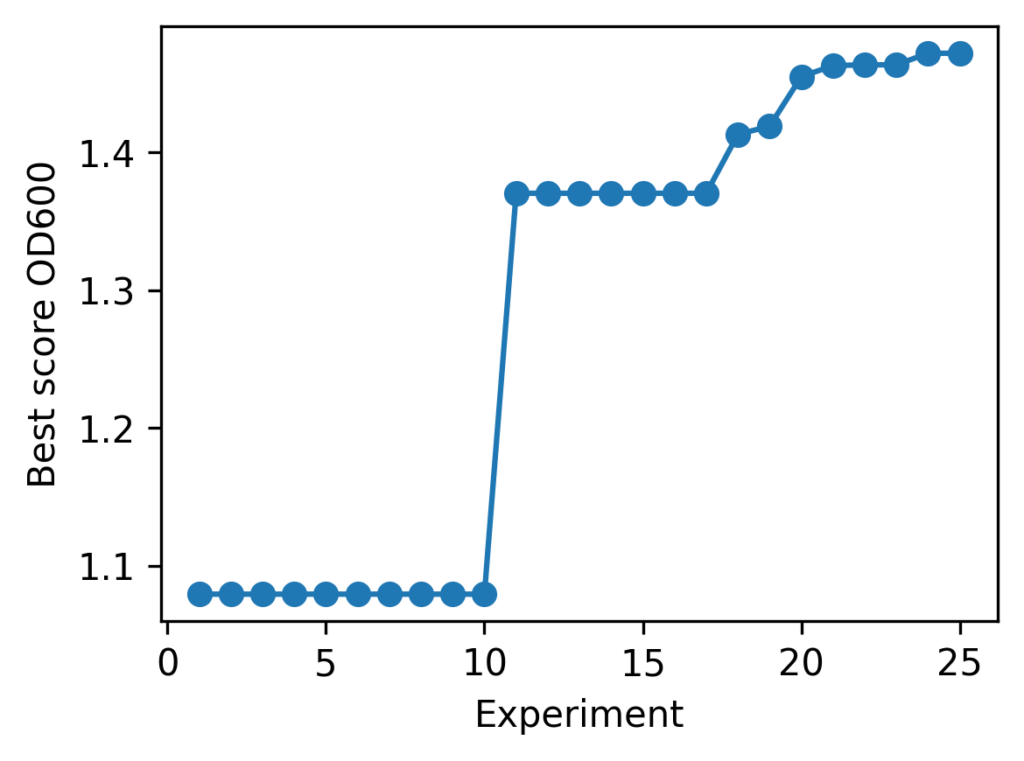
結果としては、以下の通りの培地組成が最適解として探索されました。

■逐次最適化との比較

ここまで、バッチ最適化の実装例と最適化結果を紹介してきました。 では、1条件ずつの逐次最適化とバッチ最適化はどのように違うのでしょうか。
同じ「細胞くん」を対象に最適化を行った結果を比べると、その差が明確になります。以下は、前回の逐次最適化（左）と今回のバッチ最適化（右）の結果です。

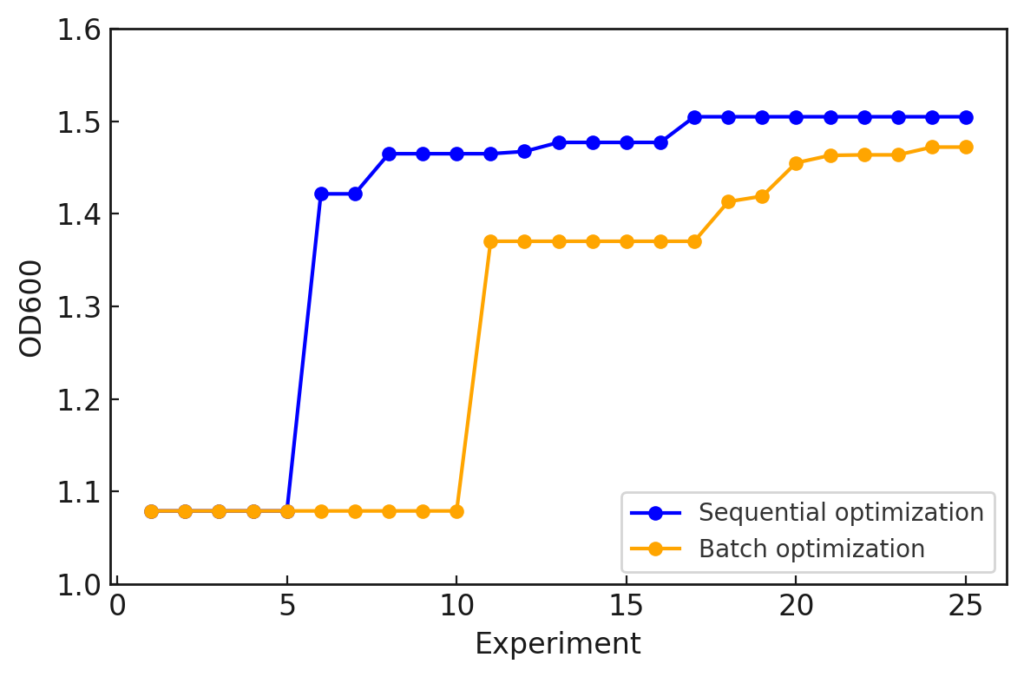
1バッチでの逐次最適化の方が探索が早く収束し、性能もやや高いことが分かります。これは1バッチでの逐次最適化では1実験ごとにモデルを更新できるため、探索効率が高いからです。一方で、バッチ最適化は並行実験が可能ですが、その分モデルの更新頻度が少なくなるため、探索効率は下がります。
ただし、現実の研究では「1回の培養に1ヶ月かかる」といった状況もあり、その場合は1バッチでの逐次最適化は非現実的です。実験効率を考慮すると、バッチ最適化が実務的には有用になります。つまり、探索精度と実験効率のトレードオフが存在します。

研究環境に応じてどちらを優先するべきかが決まります。今回は、バッチ最適化の実装例と１バッチでの逐次最適化との比較を通じて、その特徴を紹介しました。本記事の細胞挙動を模倣した一連のシミュレーションで、ライフサイエンス分野での応用イメージを持っていただければ幸いです。

ライフサイエンスでの効率的な条件最適化ならエピストラ

エピストラでは、ライフサイエンス分野に特化した実験条件最適化AI 「Epistra Accelerate」 を提供しています。オープンソースのベイズ最適化ライブラリと比べて最適化性能は約50％向上しており、より効率的に収量や品質の向上、コスト削減を実現します（Epistra Accelerate の詳細はこちら）。

これまでに 60件以上の条件最適化 を支援し、培養条件や製造プロセスにおいて業界トップクラスの成果を積み重ねてきました（実績の詳細はこちら）。

条件最適化に関する課題をお持ちの方は、ぜひお気軽にご相談ください。

実行環境について

本ページ記載のプログラムは Google Colab を用いて動作確認しています。
再現性を確保するため、Python のバージョンおよび主要ライブラリのバージョンを以下に記載します。

最終動作確認日：2025年09月30日

Python バージョン

Python 3.10.12 （Google Colab デフォルト）

使用ライブラリのバージョン