培地成分を対象としたベイズ最適化の活用入門

■はじめに

あらゆる産業で、生産性を上げるために素材の見直し、モデルの高度化、ワークフローの改善といった取り組みが絶えず行われています。特に、仕組みがよく分かっていない複雑なブラックボックス型のシステムでは、最適な条件を見つけるまでにかなりの時間とコストがかかります。生物はその典型で、現代バイオロジーが発展した今でも、「この環境や培地成分を足したらどう動くか？」を正確に予測するのはまだまだ難しいものです（モデル生物なら多少は見通しが立ちますが）。

こうした事情もあって、バイオ分野ではシミュレーション実験が難しい上に、実験そのものも高コストという問題から、大量のデータを集めて片っ端から試すようなやり方は現実的ではないです。そのため、これまでは専門家の経験や勘に基づいた「知見ベースの最適化」が主流でした。しかし、バイオ製造がどんどん高度化するにつれて、こうした人間の知見だけでは限界が見え始め、パラメータも複雑化して一筋縄ではいかなくなっています。

そこで今、「できるだけ少ない実験で最大の成果を出したい」というニーズが急速に高まっています。

そんな中で注目されているのがベイズ最適化です。マテリアルインフォマティクスなどの分野ではすでに活用が進んでいて、その効果も実証されています。

とはいえ、バイオ分野では導入が始まったばかりで、参考になる事例や資料は少ない上、培地最適化に関わるバイオ研究者の多くはコンピュータサイエンスに馴染みがないため、「ベイズ最適化？なにそれ？」という感覚の人も多いと思います。

そこで本稿では、培地成分量に対する細胞の挙動をイメージした関数を用い、ベイズ最適化の手法と得られる結果のイメージを説明します。実用上は一度に複数条件を提案するバッチベイズ最適化が主流ですが、説明を分かりやすくするために、ここではまず逐次的に条件を更新する逐次最適化の例を取り上げます。そのうえで、得られる結果のイメージを示しながら、バイオ分野における活用の可能性を考えていきます。

■細胞挙動を再現した関数の作成

先ほど「ブラックボックス」と説明しましたが、まさに細胞はブラックボックス関数の代表例と言えます。たとえば、炭素源としてのグルコース量を x g、窒素源としての NH₄Cl を y g とします。このとき、細胞の生育（OD₆₀₀）を f(x, y) として表すことができます。つまり、細胞の増殖は「入力した x と y に応じて出力される値」として扱えるわけです。

本稿では説明をシンプルにするため、グルコース量を x、窒素源 NH₄Cl を y として、ある挙動を示す2次元関数（ここでは愛称として「細胞くん」と呼びます）を定義します。実験に携わっている方なら想像しやすいと思いますが、培地成分を増やせば増やすほど単純に増殖が伸びるわけではありません。実際には、成分同士の複雑な相互作用によって、多様な増殖パターンが現れます。

ここでは、そのイメージを反映した関数 f(x, y) を作成しました。この関数に基づく細胞くんは次のような挙動を示します (以下の図は真の分布。これが事前に知れていれば苦労はない)。

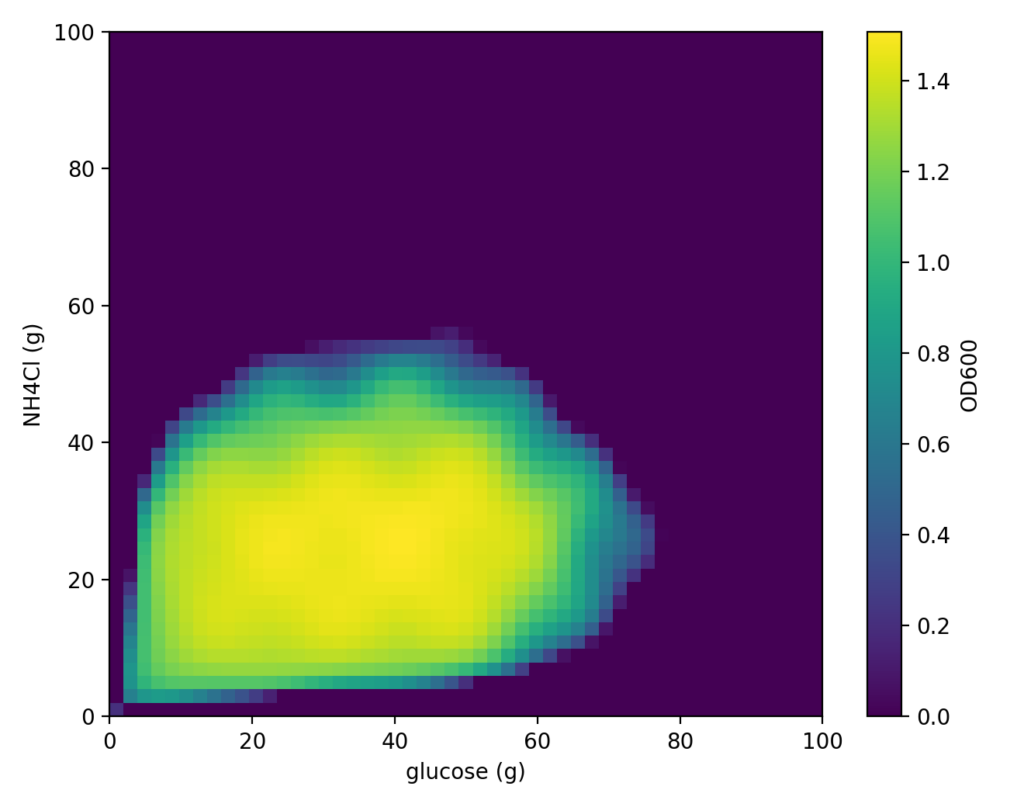
ベイズ最適化では、最初に少数の実験データを取得してから探索を始めます。今回は、その初期実験として「細胞くん」を以下の条件で培養するシミュレーションを行いました。

• x = グルコース量（g）
• y = NH₄Cl量（g）

実験条件（x［g］, y［g］）は次の5通りです：

(5.0 g, 5.0 g), (5.0 g, 95.0 g), (95.0 g, 5.0 g),

(95.0 g, 95.0 g), (50.0 g, 50.0 g)

この結果から、細胞くんは以下のような培養挙動を示すことが分かりました。

以降のスクリプトは、次のリンクから実行できます。

まず解析に必要なパッケージ群をインストールします。

!pip -q install imageio openpyxl scikit-optimize

!pip -q install imageio openpyxl scikit-optimize

このデータを以下のようにpython上で利用できるデータフレームとして読み込みます。

import pandas as pd
from io import StringIO

csv_text = """Glucose (g),NH4Cl (g),0D600
5.0,5.0,1.079207
5.0,95.0,0.000000
95.0,5.0,0.000000
95.0,95.0,0.000000
50.0,50.0,0.510030
"""

# 文字列CSV → DataFrame
df_raw = pd.read_csv(StringIO(csv_text))

# 列名を標準化：x=glucose, y=NH4Cl, od=OD600
seed_df = df_raw.rename(columns={"Glucose (g)": "x", "NH4Cl (g)": "y", "0D600": "od"})

# 確認
seed_df

import pandas as pd
from io import StringIO

csv_text = """Glucose (g),NH4Cl (g),0D600
5.0,5.0,1.079207
5.0,95.0,0.000000
95.0,5.0,0.000000
95.0,95.0,0.000000
50.0,50.0,0.510030
"""

# 文字列CSV → DataFrame
df_raw = pd.read_csv(StringIO(csv_text))

# 列名を標準化：x=glucose, y=NH4Cl, od=OD600
seed_df = df_raw.rename(columns={"Glucose (g)": "x", "NH4Cl (g)": "y", "0D600": "od"})

# 確認
seed_df

読み込まれた結果として、次のように表示されます。

　x	　　y	　　od
0	5.0	　5.0	　1.079207
1	5.0	　95.0　0.000000
2	95.0	5.0	　0.000000
3	95.0	95.0	0.000000
4	50.0	50.0	0.510030

　x	　　y	　　od
0	5.0	　5.0	　1.079207
1	5.0	　95.0　0.000000
2	95.0	5.0	　0.000000
3	95.0	95.0	0.000000
4	50.0	50.0	0.510030

続いて、ベイス最適化に用いるモデルを準備します

from od_objective_2d import ODObjective2D, BOUNDS2D
from skopt import Optimizer
from skopt.space import Real
import numpy as np

# 目的関数（細胞くん）の生成
obj = ODObjective2D()

# 探索範囲（x=glucose, y=NH4Cl の下限/上限）を定義
space = [Real(BOUNDS2D["x"][0], BOUNDS2D["x"][1], name="x"),
         Real(BOUNDS2D["y"][0], BOUNDS2D["y"][1], name="y")]

# ベイズ最適化器の生成
opt = Optimizer(
    dimensions=space,
    base_estimator="GP",  # 内部の代理モデルにガウス過程 (Gaussian Process) を使用
    acq_func="EI",  # 獲得価値関数：改善期待値 (Expected Improvement) を使って「次に測るべき点」を決めます。
    random_state=7
)

best_od = -np.inf
best_xy = (None, None)
rows = []
for i, r in seed_df.reset_index(drop=True).iterrows():
    xi, yi, odi = float(r["x"]), float(r["y"]), float(r["od"])
    opt.tell([xi, yi], -odi)
    if odi > best_od:
        best_od, best_xy = odi, (xi, yi)
    rows.append({"iter": i+1, "phase": "seed", "x": xi, "y": yi, "od": odi,
                 "best_so_far": best_od, "best_x": best_xy[0], "best_y": best_xy[1]})

from od_objective_2d import ODObjective2D, BOUNDS2D
from skopt import Optimizer
from skopt.space import Real
import numpy as np

# 目的関数（細胞くん）の生成
obj = ODObjective2D()

# 探索範囲（x=glucose, y=NH4Cl の下限/上限）を定義
space = [Real(BOUNDS2D["x"][0], BOUNDS2D["x"][1], name="x"),
         Real(BOUNDS2D["y"][0], BOUNDS2D["y"][1], name="y")]

# ベイズ最適化器の生成
opt = Optimizer(
    dimensions=space,
    base_estimator="GP",  # 内部の代理モデルにガウス過程 (Gaussian Process) を使用
    acq_func="EI",  # 獲得価値関数：改善期待値 (Expected Improvement) を使って「次に測るべき点」を決めます。
    random_state=7
)

best_od = -np.inf
best_xy = (None, None)
rows = []
for i, r in seed_df.reset_index(drop=True).iterrows():
    xi, yi, odi = float(r["x"]), float(r["y"]), float(r["od"])
    opt.tell([xi, yi], -odi)
    if odi > best_od:
        best_od, best_xy = odi, (xi, yi)
    rows.append({"iter": i+1, "phase": "seed", "x": xi, "y": yi, "od": odi,
                 "best_so_far": best_od, "best_x": best_xy[0], "best_y": best_xy[1]})

ODObjective2Dは細胞くんの挙動を表す関数です（OD を出力です）。今回では、モデルが提案した条件の結果を評価するために、このモデルを利用します。注意点としては、実運用では関数は準備できないので、このプロセスはスキップして、実測値を入力すればいいです。

Optimizer(...)：ベイズ最適化器を作成。

• base_estimator="GP"：内部の代理モデルにガウス過程 (Gaussian Process) を使用。
• acq_func="EI"：改善期待値 (Expected Improvement) を使って「次に測るべき点」を決めます。

ここまでで準備は完了です！実際に次のように動かしてみます。

n_iters = 20  # 実験の総回数

print("\n=== ベイズ最適化を開始（実験設計→実験→モデルに問い合わせ） ===")
for t in range(1, n_iters+1):
    # 1) ask: 次に測るべき点を1つ提案
    x_next, y_next = opt.ask()
    print(f"[BO iter {t}] 提案点: Glucose={x_next:.3f}, NH4Cl={y_next:.3f}")

    # 2) 実験（今回デモなので関数を呼ぶ。実運用ではここを実測に置換）
    od_measured = float(obj(x_next, y_next))
    print(f"            測定 OD= {od_measured:.6f}")

    # 3) tell: 新しい観測を BO に渡す
    opt.tell([x_next, y_next], -od_measured)

    # 4) ベストの更新チェック
    improved = ""
    if od_measured > best_od:
        best_od, best_xy = od_measured, (x_next, y_next)
        improved = "  ← ★ベスト更新！"

    rows.append({
        "iter": len(rows)+1, "phase": "bo",
        "x": x_next, "y": y_next, "od": od_measured,
        "best_so_far": best_od, "best_x": best_xy[0], "best_y": best_xy[1],
    })
    print(f"            現在のbest = {best_od:.6f} @ {best_xy}{improved}")

n_iters = 20  # 実験の総回数

print("\n=== ベイズ最適化を開始（実験設計→実験→モデルに問い合わせ） ===")
for t in range(1, n_iters+1):
    # 1) ask: 次に測るべき点を1つ提案
    x_next, y_next = opt.ask()
    print(f"[BO iter {t}] 提案点: Glucose={x_next:.3f}, NH4Cl={y_next:.3f}")

    # 2) 実験（今回デモなので関数を呼ぶ。実運用ではここを実測に置換）
    od_measured = float(obj(x_next, y_next))
    print(f"            測定 OD= {od_measured:.6f}")

    # 3) tell: 新しい観測を BO に渡す
    opt.tell([x_next, y_next], -od_measured)

    # 4) ベストの更新チェック
    improved = ""
    if od_measured > best_od:
        best_od, best_xy = od_measured, (x_next, y_next)
        improved = "  ← ★ベスト更新！"

    rows.append({
        "iter": len(rows)+1, "phase": "bo",
        "x": x_next, "y": y_next, "od": od_measured,
        "best_so_far": best_od, "best_x": best_xy[0], "best_y": best_xy[1],
    })
    print(f"            現在のbest = {best_od:.6f} @ {best_xy}{improved}")

n_itersはモデルによる条件提案とその評価を行うプロセスは何回行うかに対応しています。今回はin silicoなので無限にできますが、現実では予算によって制約される値です。

この結果、次の出力が得られます。

=== ベイズ最適化を開始（実験設計→実験→モデルに問い合わせ） ===
[BO iter 1] 提案点: Glucose=22.734, NH4Cl=31.897
            測定 OD= 1.421598
            現在のbest = 1.421598 @ (22.733907982646524, 31.89722257734033)  ← ★ベスト更新！
[BO iter 2] 提案点: Glucose=97.822, NH4Cl=45.558
            測定 OD= 0.000000
            現在のbest = 1.421598 @ (22.733907982646524, 31.89722257734033)
[BO iter 3] 提案点: Glucose=30.801, NH4Cl=26.387
            測定 OD= 1.464924
            現在のbest = 1.464924 @ (30.80127651877394, 26.387083903789872)  ← ★ベスト更新！
           

=== ベイズ最適化を開始（実験設計→実験→モデルに問い合わせ） ===
[BO iter 1] 提案点: Glucose=22.734, NH4Cl=31.897
            測定 OD= 1.421598
            現在のbest = 1.421598 @ (22.733907982646524, 31.89722257734033)  ← ★ベスト更新！
[BO iter 2] 提案点: Glucose=97.822, NH4Cl=45.558
            測定 OD= 0.000000
            現在のbest = 1.421598 @ (22.733907982646524, 31.89722257734033)
[BO iter 3] 提案点: Glucose=30.801, NH4Cl=26.387
            測定 OD= 1.464924
            現在のbest = 1.464924 @ (30.80127651877394, 26.387083903789872)  ← ★ベスト更新！
           

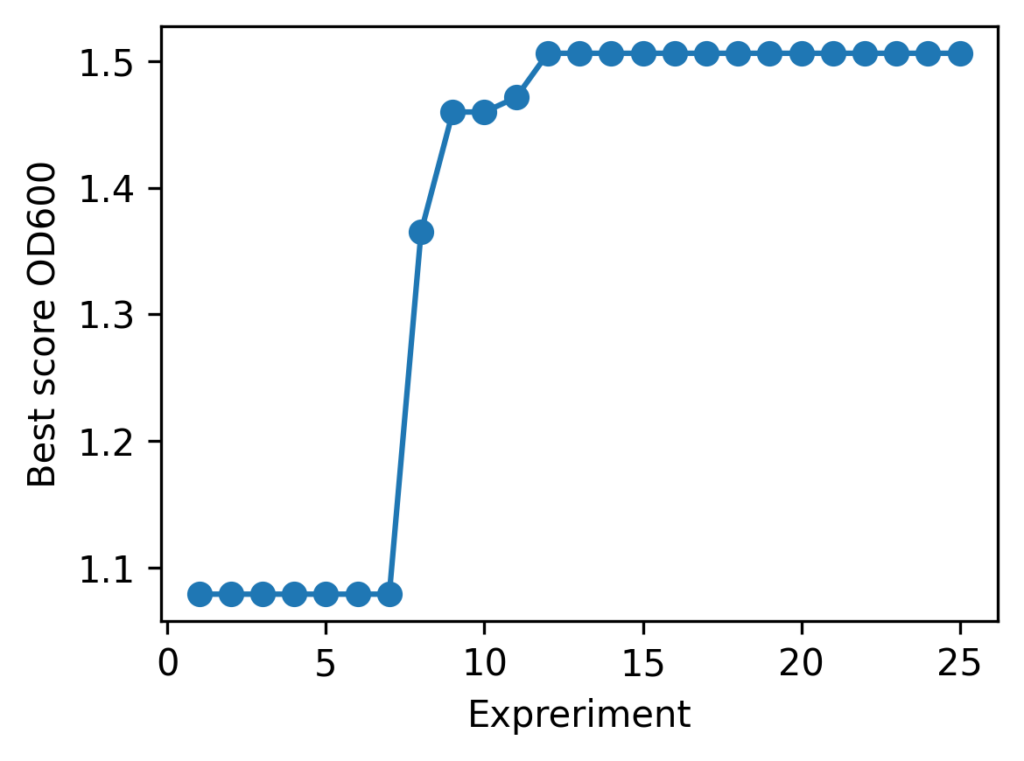
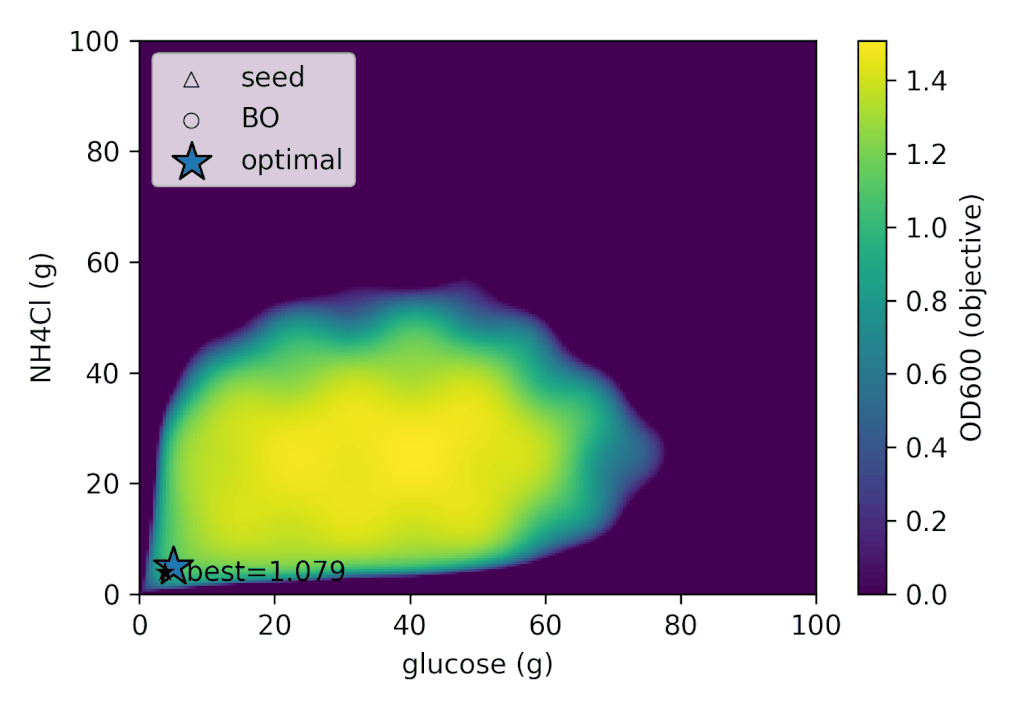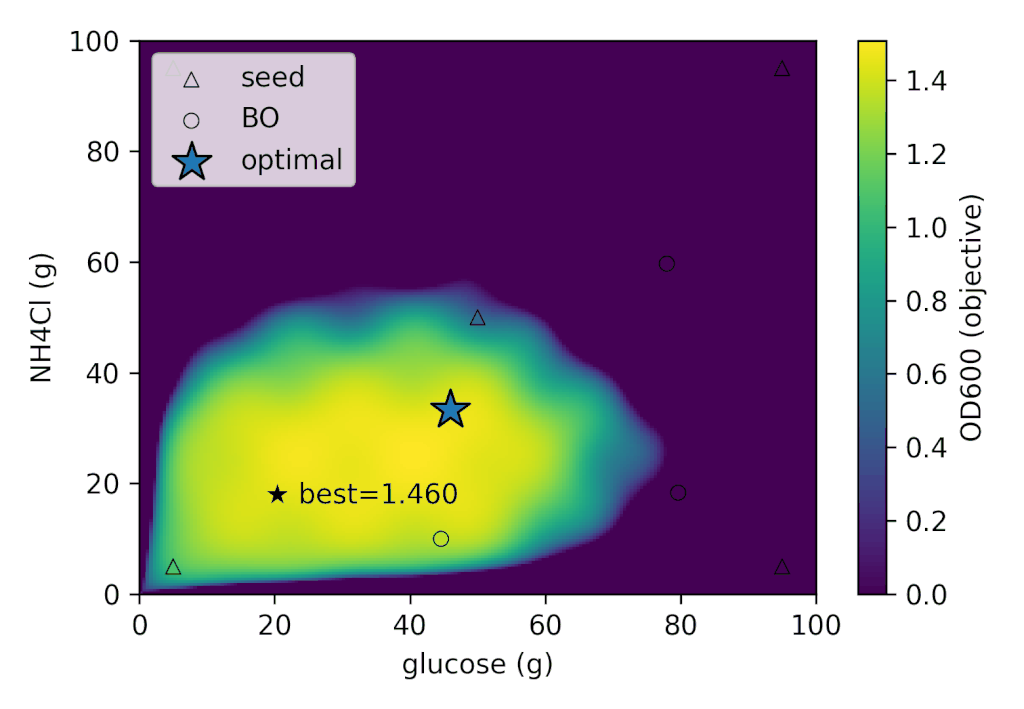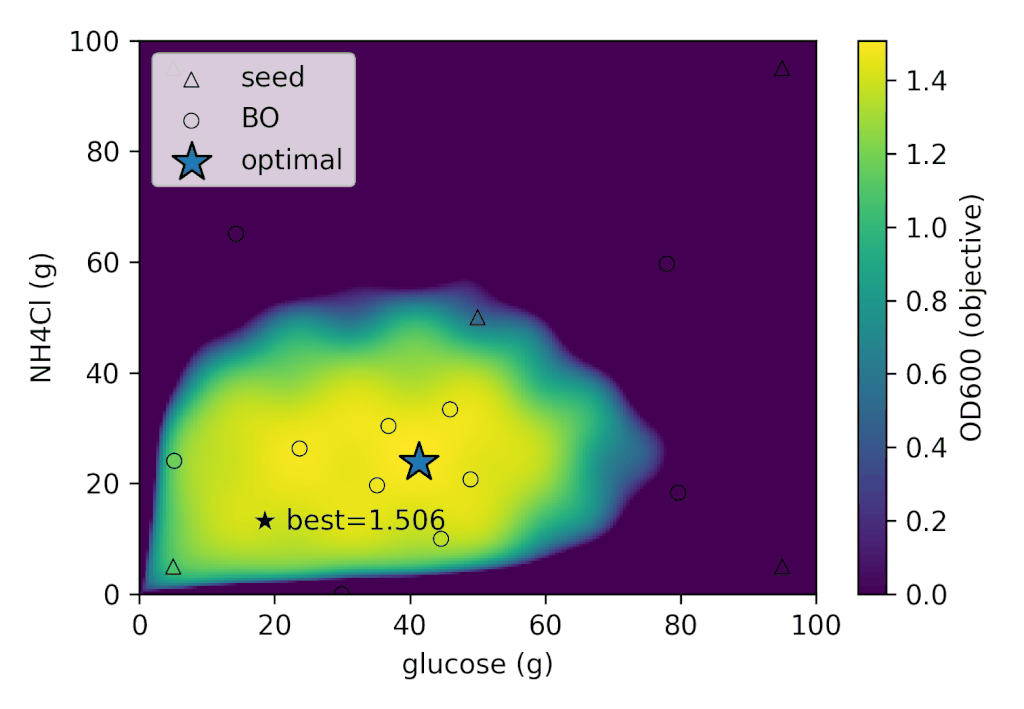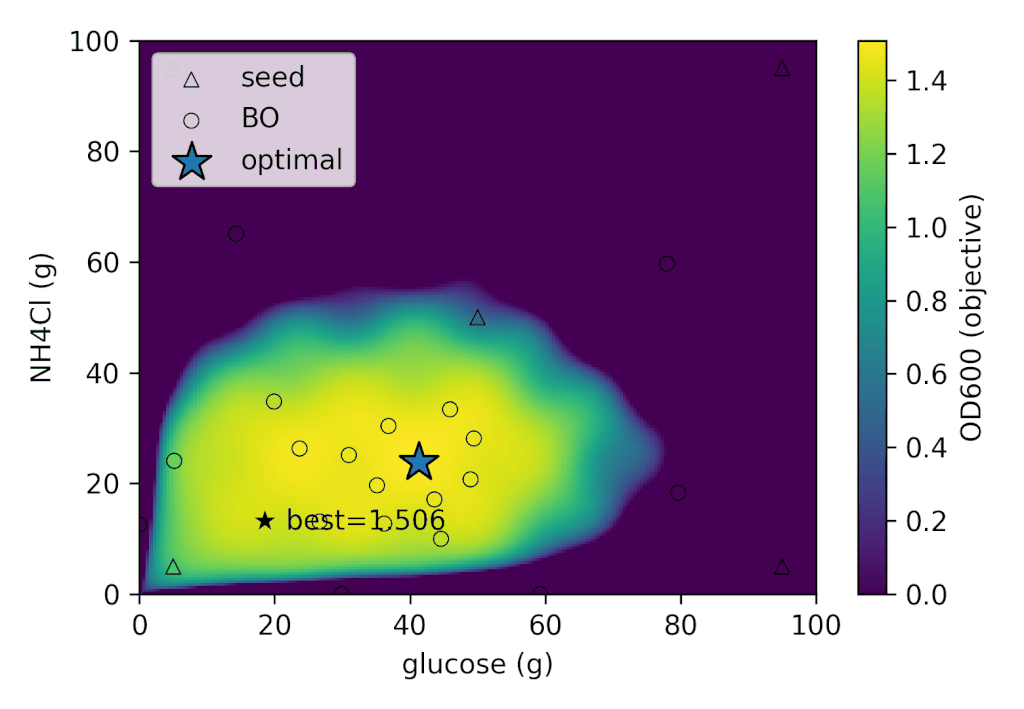
左: 各ラウンドごとの実験結果の推移, 右: 細胞くんの応答分布における各実験の探索位置

今回の細胞くんの挙動では、初期実験を含めて、合計12回の実験で

という実験条件が得られました。細胞くんはかなりグルコース要求性が高いですね。

このように、一見ハードルが高く見えるベイズ最適化も、少しのコーディングで実務に活用できます。本記事が皆さんの培地最適化の取り組みに、少しでもお役に立てば幸いです。

今回は説明を簡潔にするため、2つのパラメータによる単純な最適化を例に挙げましたが、実際の課題の多くはより高次元です。また、生育だけでなく物質生産量や品質などを同時に考慮する多目的最適化が求められる場面も少なくありません。
弊社では、高性能な最適化システム「Epistra Accelerate」を提供しています。個別事例にも対応可能ですので、より高度な最適化や実データへの適用についてご相談があれば、ぜひお気軽にお問い合わせください。

今回の例は、各ラウンドごとに1回づつ実験条件を提案し、評価する形式でした。しかし、一般には毎回のラウンドでは複数回の条件を並行して比較することが多いと思います。このようなパターンは、バッチベイズ最適化と呼称されています。
次回は、バッチベイズ最適化を用いた、細胞くんの培地最適化に挑戦していきましょう。

（次回）培地成分を対象としてベイズ最適化の活用入門 (バッチ最適化) はこちら！

ライフサイエンスでの効率的な条件最適化ならエピストラ

エピストラでは、ライフサイエンス分野に特化した実験条件最適化AI 「Epistra Accelerate」 を提供しています。オープンソースのベイズ最適化ライブラリと比べて最適化性能は約50％向上しており、より効率的に収量や品質の向上、コスト削減を実現します（Epistra Accelerate の詳細はこちら）。

これまでに 60件以上の条件最適化 を支援し、培養条件や製造プロセスにおいて業界トップクラスの成果を積み重ねてきました（実績の詳細はこちら）。

条件最適化に関する課題をお持ちの方は、ぜひお気軽にご相談ください。

実行環境について

本ページ記載のプログラムは Google Colab を用いて動作確認しています。
再現性を確保するため、Python のバージョンおよび主要ライブラリのバージョンを以下に記載します。

最終動作確認日：2025年11月10日

Python バージョン

Python 3.10.12 （Google Colab デフォルト）

使用ライブラリのバージョン